يهدف التحليل الإحصائي إلى استخراج معاني محددة تتعلق بالموضوع البحثي الذي يتناوله الباحث، وذلك تحقيقًا لأهداف البحث؛ وحيث أن التحليل الإحصائي هو عبارة عن مجموعة من الأرقام يتم ملاحظة العلاقات بينها ثم تفسيرها، فإن من أهم الاعتبارات هي النقاط التي تتمحور حولها القيم والتي تسمى مقاييس النزعة المركزية، وكذلك مقدار الابتعاد عن تلك النقاط، والتي تسمى مقاييس التشتت.
وتبرز أهمية مقاييس النزعة المركزية والتشتت في البحث العلمي في كونها تعطي صورة متكاملة حول الظاهرة موضوع البحث؛ حيث توضح ميل عينة البحث إلى الارتكاز حول نقاط محددة، وكذلك القيم التي تبتعد عن تلك النقاط، سنتعرف أكثر عن مقاييس النزعة المركزية في الإحصاء من خلال هذا المقال.
ما هي مقاييس النزعة المركزية - Measures of Central Tendency
تعتبر مقاييس النزعة المركزية في الإحصاء هي عبارة عن مجموعة من المقاييس تصف نقطة تجمع المشاهدات، وقد تأسس هذا النوع من المقاييس على يد الباحث الإنجليزي فرانسيس جالتون، ومن أهم مقاييس النزعة المركزية المتوسط الحسابي، والوسيط، وكذلك المنوال.
لماذا تُستخدم مقاييس النزعة المركزية؟
تدل كافة مقاييس النزعة المركزية على ميل كافة البيانات؛ وذلك للتجمع حول القيم المركزية جميعها، ومقاييس النزعة المركزية في الإحصاء تعتبر من أهم خصائص التوزيعات النظرية، ويحدث في كثير من الأحيان أن يتناقض الاتجاه الخاص بالمركزية الخاصة بالتوزيع، وذلك عند تشتيته.
ترجع الأهمية الكبيرة لمقاييس التشتت الخاصة بالنزعة المركزية وكذلك فإن أبرز استخدامات مقاييس النزعة المركزية أنها وسيلة جيدة في تحليل كافة البيانات، وذلك من خلال القدرة الكبيرة على تحديد الميل الخاص بالنزعة المركزية، وذلك من خلال تحديد هل هي قوية أم ضعيفة، وتستخدم المقاييس كذلك في الوصف، وكذلك فإن لها دور كبير في حل مشكلة التباين الإحصائي.
تعرف كذلك على: التحليل الإحصائي في البحث العلمي من خلال هذا المقال
أهمية مقاييس النزعة المركزية
مقاييس النزعة المركزية تتيح لنا التعبير عن التوزيع بدرجة تمثل المعدل أو الدرجة الخطية، أو الدرجة التي تمثل التوزيع؛ حيث أن الدرجة التي يتم حسابها للنزعة المركزية تمثل تمركز التوزيع أو ثقله وهناك العديد من الأساليب المستخدمة لتمثيل النزعة المركزية، غير إننا سوف نتناول ثلاثة منها هي الأكثر استخدامًا، وهي الوسط، الوسيط، والمنوال التي يمكن الاستفادة منها وفقًا للهدف ولطبيعة البيانات.
أولًا: أهمية الوسط الحسابي
بإمكانك أن تقوم بحساب الوسط الحسابي من خلال جمع كافة القيم أو المفردات ومن ثم قسمة هذه القيم على العدد الخاص بها، ويمكننا توضيح هذه الأهمية في صورة مجموعة من النقاط كالتالي:
1- بإمكان الوسط الحسابي بحساب كافة المفردات المتواجدة في بحثك.
2- ستحصل من خلاله على متوسط دقيق للقيم المتواجدة معك.
3- يتكون من مجموعة من القيم العددية؛ مما يسهل إجراء الحسابات.
4- يعتبر حساب الوسط الحسابي في غاية السهولة، ويعتبر مناسبًا في حالة القيم الكثيرة.
ثانيًا: أهمية الوسيط
الوسيط من اسمه يعتبر هو القيمة المتوسطة بين كافة القيم التي نقوم بترتيبها، وذلك إذا قمت بالترتيب في صورة تصاعدية أو إذا قمت بالترتيب في صورة تنازلية، والأهمية الخاصة بالوسيط تتمثل فيما يلي:
1- يمكن حساب الوسيط بطريقة بسيطة وواضحة.
2- بإمكانك أن تقوم بإجراء أي عملية حسابية عليه بسهولة.
3- يستخدم إذا كان هناك قيم شاذة أو متطرفة في البيانات.
ثالثًا: أهمية المنوال
يعتبر المنوال هو القيمة التي تتكرر كثيرًا بين كافة القيم المتواجدة لديك، ويمكن أن يجد الباحث أكثر من قيمة تتكرر في القيم المتواجدة لديه، وفي هذه الحالة سيكون هناك أكثر من منوال، وترجع أهمية المنوال فيما يلي:
1- يعتبر المنوال من أكثر مقاييس النزعة المركزية سهولة.
2- بإمكانك أن تفهم المنوال بسهولة ووضوح.
3- يمكن استخدام الرسومات الهندسية لتعيينه.
4- يتم استخدامه عند وجود القيم الشاذة.
تعرف على استخلاص نتائج البحث العلمي من خلال هذا المقال
اهداف مقاييس النزعة المركزية
1- جمع كافة البيانات التي تتسم بأنها عددية من خلال العينات بسهولة.
2- جمع كافة البيانات العددية في وقت قصير، وبجهد قليل.
3- العمل على تمثيل كافة البيانات في قيمة واحدة.
4- التعبير عن العينة الخاصة بالدراسة، خصوصًا العينات الكبيرة.
5- مقارنة جميع البيانات ببعضها بطريقة سهلة وبسيطة.
6- التعرف على جميع النتائج الخاصة بالأبحاث والرسائل.
تعرف كذلك على الأساليب الإحصائية في البحث العلمي من خلال هذا المقال
ما هي أنواع مقاييس النزعة المركزية؟
سنتعرف من خلال هذه الفقرة على أهم أنواع مقاييس النزعة المركزية في الإحصاء، وأهم هذه الأنواع ما يلي:
أولًا: المنوال
يعتبر المنوال أول نوع من أنواع مقاييس النزعة المركزية في أي توزيع تكراري غالبا ما تظهر درجة تتكرر بشكل أكبر من غيرها، وهي ما يسمى المنوال فالمنوال هو الدرجة الأكثر تكرارا في التوزيع، ما رأيك أن نتعرف أكثر على المنوال من خلال مثال بسيط؟
مثال على المنوال
في الدرجات: (1، 2، 3، 3، 5، 6، 7) يكون المنوال هو 3 لأنها تكررت أكثر من الدرجات الأخرى، أما في التوزيعات ذات الفئات، فإن المنوال هو مركز الفئة الأكثر تكرارًا.
وهناك حالات فيها منوالين في توزيع واحد كما في الدرجات أدناه وعندها يسمى التوزيع ذا منوالين: (6، 7، 8، 8، 8، 9، 9، 10، 10، 10، 11، 12)، والمنوالين هنا هما الدرجتان 8، 10 نادرًا ما يستفيد الباحث من ولكنه مفيد في بعض الحالات.
ثانيًا: الوسيط
هو الدرجة التي تقع في وسط القيم بعد ترتيبها بمعنى أن نصف الدرجات تكون أقل منها والنصف الأخر أعلى منها، ففي أي توزيع يكون عدد القيم الأعلى من الوسيط مساويًا لعدد القيم الأعلى منه، وفي الدرجات التي يكون عددها فرديا يكون الوسيط هو الدرجة الوسطى.
مثال على الوسيط
ففي الدرجات (8، 9، 11، 14، 15) تكون الدرجة 11 هي الوسيط أما في الحالة التي يكون فيها عدد الدرجات زوجيا فإن الوسيط هو حاصل قسمة مجموع الـدرجتين الوسطيتين على 2 بعد أن يتم ترتيب الدرجات، ففي الدرجات (2، 3، 5، 9، 11، 16) ناتج قسمة (5 + 9) ÷ 2 = (7).
ويجب ترتيب القيم قبل أن يتم حساب الدرجة الوسيطة، ففي الدرجات (5 ،9 ،2 ،16 ،4، 6) علينا أن نرتبها أولاً فتكون (2 ، 3 ، 4 ، 5 ، 6 ، 9 ،16) والوسيط هنا الدرجة (5).
وغالبا ما نستخدم الوسيط في حالة وجود درجات متطرفة، ففي الدرجات 1، 2، 3، 5، 200 يكون الوسيط أفضل؛ لأنه لا يتأثر بالقيمة المتطرفة كما هو الحال في الوسط.
ثالثًا: الوسط
وهو الأكثر استخداما عادة، وهو ما يطلق عليه بالمعدل فهو ببساطه مجموع الدرجات مقسوما على عددها، ويعتبر الوسط من أهم مقاييس النزعة المركزية في الإحصاء وأكثرها سهولة.
وعند وجود انحرافات كبيرة عن الوسط كما في المثال السابق لا يكون الوسط مناسبا، ويكون الوسيط أقرب تمثيلًا لمجموع الدرجات، ففي الحالة أعلاه يكون الوسيط 4 وهو أقرب لتمثل الدرجات من الوسط (22.4).

ما هي أنواع مقاييس التشتت في البحث العلمي؟
إن التعبير عن مجموعة بمقاييس النزعة المركزية في الإحصاء يعني النظر إلى المجموعة ككل بغض النظر عن الاختلافات بين الأفراد، وعلى الرغم من أن هذا الأسلوب يزودنا ببعض المعلومات المهمة عن المجموعة، إلا أنه في نفس الوقت يخفي خصائص المجموعة.
فاستخدام الوسط الحسابي مثلًا يكون معبرًا عندما تكون قيم التوزيع متقاربة من بعضها البعض، إلا أن كثير من الإحصائيات يكون هناك حالات بعيدة عن الوسط؛ حيث تكون هناك بعض القيم الشاذة، ومن ثم تكون الصورة التي يعطيها الوسط الحسابي غير دقيقة.
فمثلا المجموعة التي وسطها 50 تضم أفرادا قد حصلوا على نفس الدرجة أم أن هناك تباين كبير بحيث أن أحدهم حصل على 100 فيما حصل آخر على صفر، ففي المجموعة (50، 50 ، 50 ،50 ، 50) تضم خمس أفراد وأن الوسط (50).
فيما تضم المجموعة الآتية (100 ، 70 ، 50 ،30) خمس أفراد وبمتوسط مقداره خمسين أيضا، ومن ذلك يتضح أن مقاييس النزعة المركزية في الإحصاء وحده لا يفي بالغرض إذ لا يوضح الخصائص الأخرى للمجموعة من حيث تجانس الأفراد وعدمه.
فالمجموعة الأولى متجانسة تماما، بينما نجد أن هناك تجانسا أقل في المجموعة الثانية، أن موضوع التجانس وعدم التجانس هذا يمكن الحصول على مؤشرات عنه إلى جانب مؤشرات النزعة المركزية باللجوء إلى واحد من مقاييس التباين، وسوف نتطرق إلى مكل من المدى والانحراف المعياري.
أولًا: المدى
المدى هو الفرق بين أعلى درجة وأقل درجة ففي الدرجات 90، 80، 60، ، 30 يكون المدى 90- 30= 60، أي أن المدى هو النطاق الذي تنحصر فيه القيم، هذا ويمكن استخدام مدى التبـاين في الحالات التي يكون هناك حاجة إلى السرعة وحالات القرارات غير المهمة نظرًا لسهولة استخراجه.
إذ على الرغم من أن المدى هو واحد من مقاييس التباين، إلا أنه غير دقيق؛ لأنه لا يأخذ بنظر الاعتبار سوى درجتين فيما يهمل الدرجات الأخرى؛ لذلك نجد أنه من النادر اللجوء إليه في الحالات التي تتطلب الدقة ويكون للقرار المتخذ أهمية.
إذ من الملاحظ بأنه مهما تغيرت الدرجات الأخرى عدا الدرجتين المتطرفتين فإن المدى سيبقى ثابتا لا يتغير، ولكنه قد يتأثر بشكل ملحوظ حين تتغير واحدة من الدرجات المتطرفة إلى أعلى أو إلى أقل.
ثانيًا: الانحراف المعياري
يستخدم في التعرف على مدى انتشار مجموعة من الدرجات. فهو أفضل المؤشرات عن مدى تجانس المجموعة، لأنه يأخذ بنظر الاعتبار كل الدرجات، كشأن الوسط بالنسبة لمقاييس النزعة المركزية في الإحصاء ولإيضاح كيفية حساب الانحراف المعياري نفترض أن لدينا توزيعًا يتكون من خمس درجات كما يأتي:
![]() أن أول خطوة لحساب الانحراف المعياري هو حساب الوسط.
أن أول خطوة لحساب الانحراف المعياري هو حساب الوسط.
![]() والخطوة الثانية هو أن نحسب مقدارا ابتعادا كل درجة من الدرجات الخمس (س) عن الوسط.
والخطوة الثانية هو أن نحسب مقدارا ابتعادا كل درجة من الدرجات الخمس (س) عن الوسط.
تعرف أكثر على مقاييس التشتت في البحث العلمي من خلال هذا المقال
مثال على حساب مقاييس النزعة المركزية
سنتناول في هذه الفقرة مثالًا على حساب مقاييس النزعة المركزية، الوسط الحسابي، الوسيط وكذلك المنوال، وهذا المثال هو:
قام مدير مراقبة الإنتاج بالتوجه إلى أحد الشركات الخاصة بالمياه؛ وذلك لفحص الأملاح المتواجدة في زجاجات المياه، وقد استخدم في ذلك 10 عبوات كعينة، والحجم الخاص بهذه العبوات كان 5 لتر.
كمية الأملاح في المياه في الزجاجات العشر 115 123 119 123 124 119 123 121 123 121 والمطلوب أن تقوم بحساب الوسط الحسابي، الوسيط وكذلك المنوال.
أولًا: حساب الوسط الحسابي
سيتم حساب الوسط الحسابي من خلال مجموع كافة القيم على عددها، وسيتم ذلك من خلال هذه المعادلة:

ثانيًا: حساب الوسيط
لحساب الوسيط سيتوجب عليك أن تقوم بحساب الرتبة الخاصة بالوسيط، ويتم ذلك من خلال جمع عدد العينات + 1 وقسمة الناتج على 2، وبذلك سيكون الناتج 5.5، ومن ثم سنقوم بحساب القيمة الخاصة بالوسيط بعد ترتيب القيم تصاعديًا.
ترتيب القيم تصاعديًا
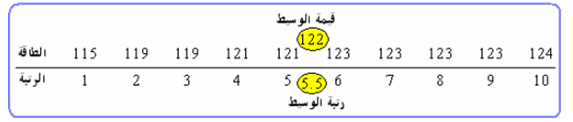
وستجد أن عدد القيم هو 10، وسيكون الوسيط في هذه الحالة هو الوسط الحسابي لكل من القيمتين 5 و 6 وذلك لأن رتبة الوسيط 5.5
معادلة حساب الوسيط
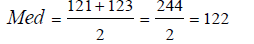
ثالثًا: حساب المنوال
المنوال سيكون هو القيمة الأكثر تكرارًا، وهذه القيمة ستكون الرقم 123، فقد تكررت هذه القيمة أكثر من القيم الأخرى.
مقارنة قيم الوسط والوسيط والمنوال
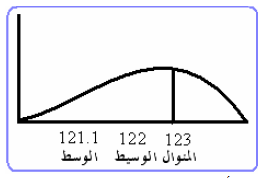
مزايا وعيوب مقاييس النزعة المركزية
سنوضح من خلال هذه الفقرة المزايا والعيوب الخاصة بمقاييس النزعة المركزية، وسيتم توضيح ذلك من خلال مجموعة من النقاط وأهم هذه النقاط ما يلي:
مميزات النزعة المركزية
1- تعتبر مقاييس النزعة المركزية ملائمة في حالة وجود الكثير من البيانات.
2- يمكن استخدام مقاييس النزعة المركزية في حالة البيانات الترتيبية.
3- ناتج مقاييس النزعة المركزية ستجده بالفعل في البيانات.
4- يعتبر هذا النوع من المقاييس مفيدًا جدًا في حالة البيانات الاسمية.
5- يعتبر استخدام هذا المقياس مفيدًا كثيرًا في حالة البيانات الترتيبية.
عيوب مقاييس النزعة المركزية
1- تعتبر البيانات أقل موثوقية وذلك لوجود أكثر من قيمة.
2- تستخدم هذه المقاييس بشكل أفضل مع القيم المتطرفة فقط.
3- قد ينتج عن هذه المقاييس أرقامًا عشرية، فتصبح النتائج أقل أهمية.
4- إذا كانت كمية البيانات قليلة أو صغيرة فذلك سيؤدي إلى عدم عمل القيم بشكل جيد.
استخدامات مقاييس النزعة المركزية في حياتنا اليومية
قد تستخدم عزيزي مقاييس النزعة المركزية في الإحصاء بشكل لا إرادي في حياتك اليومية، ومن ضمن أشكال استخدامات مقاييس النزعة المركزية ما يلي:
أولًا: اختيار نوع الفيلم المناسب
إذا ذهبت أنت وكافة أفراد عائلتك لتشاهد فيلمًا، فإنك عندما تصل إلى صالة السينما ستجد أكثر من نوع من أنواع الأفلام، فستجد فيلمًا خاصًا بالرسوم المتحركة وكذلك ستجد فيلمًا عن السيرة الذاتية وغيرها.
ففي هذه الحالة ستقوم بتحديد أعمار الأشخاص الذين يقومون بمشاهدة هذا النوع من الافلام وستجد أن هذه الأعمار تتراوح بين 6 و 13 و 15 و 17 و 60، في هذه الحالة ستقوم بحساب المتوسط أو الوسيط وستكون قيمته 22 عامًا، وبذلك ستختار فيلمًا ملائمًا مع هذا العام وبالتالي ستختار فيلمًا عن السيرة الذاتية.
ثانيًا: تجميع البيانات
إذا كنت معلمًا وترغب في تنظيم نشاط معين في الفصل الخاص بك، يجب أن تقوم في البداية بتقسيم الصف إلى مجموعتين على سبيل المثال، ويمكنك أن تختار تقيم الصف حسب الطول الخاص بالطلاب.
بعد ذلك عليك أن تقوم بترتيب جميع الطلاب حسب أطوالهم بشكل تصاعدي، فيجب أن يتم ترتيبهم هكذا 152 سم، 158 سم، 160 سم، 162 سم، 195 سم، ويحساب الوسيط لهذه القيم سيكون الناتج هو 161 سم، فقم بتقسيم كل من هم أقصر من 161 سم في مجموعة وكل من هم أطول من 161 سم في مجموعة أخرى.
ثالثًا: شراء عقار
إذا أردت أن تشتري عقارًا بإمكانك أن تستعين بمقاييس النزعة المركزية، وإنك في هذه الحالة ستلجأ إلى وسيط عقاري يقوم بعرض كافة الأسعار الخاصة بالعقارات عليك، وستجد أن الأسعار تبدأ من 30 و 32 و 40 و87 و 90 و 95 ألفًا على سبيل المثال.
في هذه الحالة يجب أن تقوم بحساب لوسيط وسيكون الوسيط 40 ألفًا، ويجب عليك ألا تختار العقارات التي يقل سعرها عن 40 ألفًا؛ وذلك لأنه لا بد من وجود عيب بها، وكذلك يجب ألا تختار العقارات التي يزيد سعرها عن 40 ألفًا؛ وذلك لأنها باهظة الثمن.
حمل كتب عن مقاييس النزعة المركزية بصيغة pdf
إذا أردت أن تقوم بتحميل مجموعة من الكتب عن مقاييس النزعة المركزية في الإحصاء - Measures of Central Tendency بإمكانك أن تضغط على الرابط، وستجد فيه الكثير من التي يمكنك تحميلها.
مقاييس النزعة المركزية والتشتت بصيغة pdf
بإمكانك أن تقوم كذلك بتحميل كتاب عن مقاييس النزعة المركزية والتشتت pdf من خلال هذا الرابط، وإذا كنت تُعد بحثًا عن مقاييس النزعة المركزية بإمكانك أن تقوم بتحميل بحث حول مقاييس النزعة المركزية pdf من خلال هذا الرابط.
وبذلك تكون قد تعرفت على معلومات كثيرة بخصوص مقاييس النزعة المركزية في الإحصاء، وإذا أردت المزيد من المساعدة أو الحصول على خدمات البحث العلمي عليك الإستعانة بـ شبكة المعلومات العربية، ويعتبر موقع شركة مكتبتك واحدًا من أهم المواقع في مجال البحث العلمي بلا منازع! تواصل معنا من خلال الواتساب على الفور.
مراجع يمكن الرجوع إليها
♦ العزاوي، رحيم يونس كرو. (2008). مقدمة في منهج البحث العلمي. عمان: دار دجلة ناشرون وموزعون
.jpg)
.jpg)